转子流量计的流量与密度的关系

流量计的基本原理是依据浮子两侧的压差形成向上的推力

即

式中

p1和p2---上、下游流体的压力；

K---压力损耗系数；

ρ---流体的密度；

v---流体通过环形通大道的流速。

若以体积流量qv替代流速v，即

v=qv/Aring

式中

Aring--浮子周围的环形面积。

由次则可得出

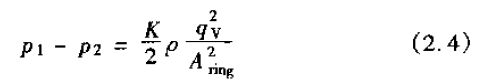
在式（2.4）中假设在入口处动力源的影响忽略不计，且浮子两侧的差压是由浮子下游动力源的损耗所造成的，那么，浮子的浮子为

W=VR(ρs-ρ)g

式中

Vs---浮子的体积；

ρs---浮子材料的比重；

g---重力加速度。

由于浮力W=As（p1-p2），式（2.5）可写成

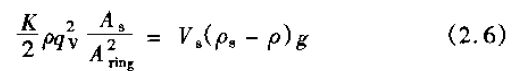
式中  As---浮子的最大截面积。

式（2.6）经整理得到

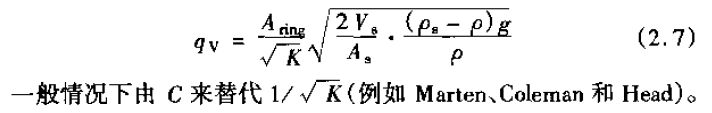
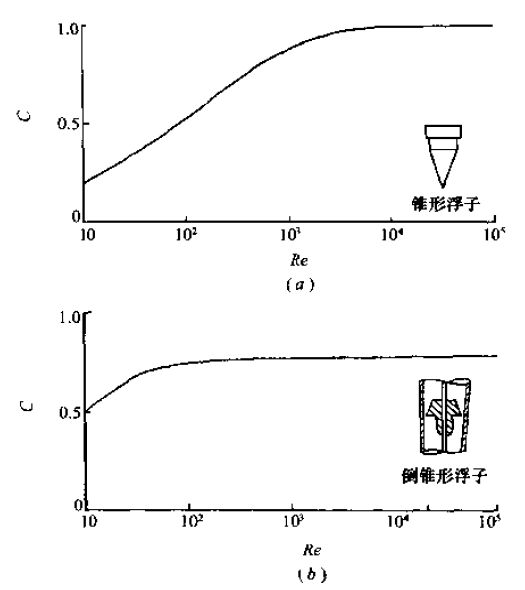
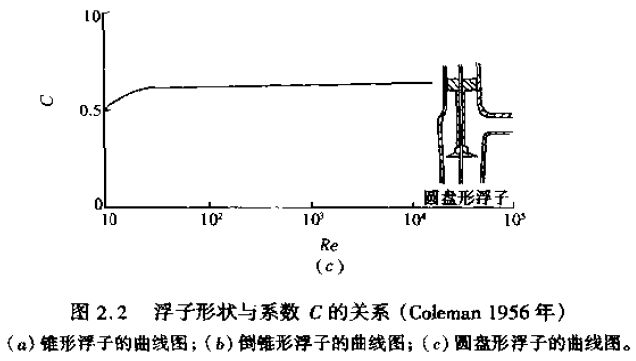
Coleman(1956年)曾对3种不同形状的浮子给出了C值，如图2.2所示，并提出，在最大流量时，C值的取值范围为从0.6(低雷诺系数敏感的浮子)到接近于1。

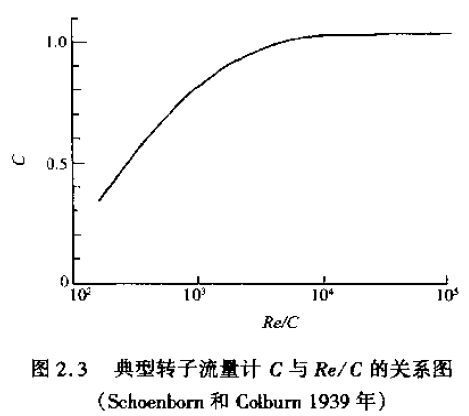
图2.2显示，在小流量时C值有所下降，这也反映了这样一个事实，即随着雷诺系数的下降，使通过一个开口的损耗系数增加(Millerl990)。在Coleman的图中可以看出各种不同的浮子形状对枯度的影响，图2.2的实质是雷诺系数对锥形浮子的C值影响最Schoenborn和Colburn(1939年)给出了C与Re/C的关系曲线图，


其中Re是以Deq为基准的雷诺系数。Deq称为等效直径，其定义为D与d的差值，如图2.3所示。当时，他们设计了一台人型高压装置，用一根钢管加上一支伸出的小棒作为指针，在一个带有刻度的玻璃窗口中运动。图2.3的曲线是在这台设备上得出的一条最佳曲线。由于考虑到浮子两侧压差产生的上升力作用，他们在实验中施加了一个能平衡液体中浮子重量的作用力。他们还注意到，在大型仪器中此曲线对流体自身的影响比小型仪器要小。

虽然对转子流量计的定量很困难，但在同样读数基础上能够把一种流体的流量值换算成另一种流体的流量值。Schoenborn和Colburn(1939年)给出了与ISA(1961b)很近似的计算公式

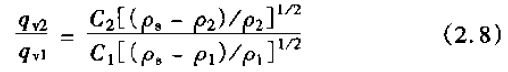
其区别在于1SA(1951b)所给的公式中省略了C2/C1，这里可认为其比值为1。Coleman(1956年)利用此公式时也把C2/C1看做1，即认为粘度的变化可忽略不计。他指出这样一个事实，假如式(2.7)的体积流量改写成质量流量，即

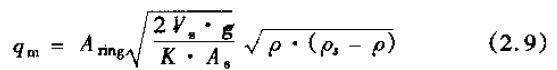
对流体密度的变化求导

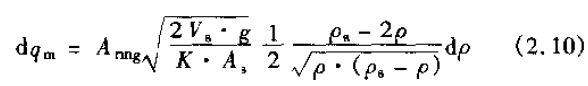
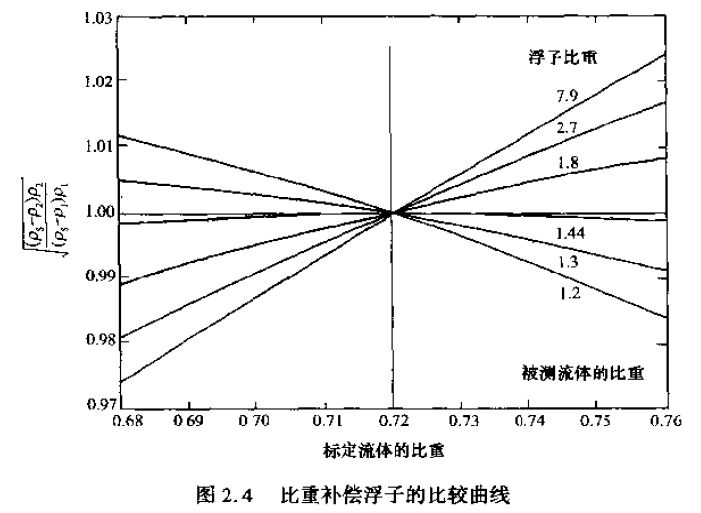
即可得出一个结论:对一个比重2倍于介质的浮子，质量流量变化为0。也就是说，它对密度变化的敏感极小(参见Head 1964年)。根据对比重为0.72的航空汽油标定的结果，图2.4表示了当流体密度变化时和在各种不同浮子情况下的密度修正系数。Head(1964年)认为，设计一种气流向下的装置，设浮子的比重为0，对它的体积流量方程进行微分运算，可以获得某些可能的进展。Head还提出，浮子的自动补偿可允许温度其他参数的变化。